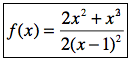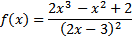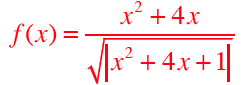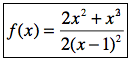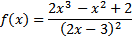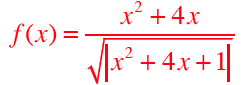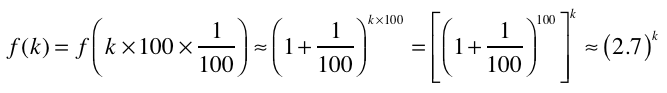Dec. 02
10:35 - 11:15
|
Application of the Derivative
of a function in one point :
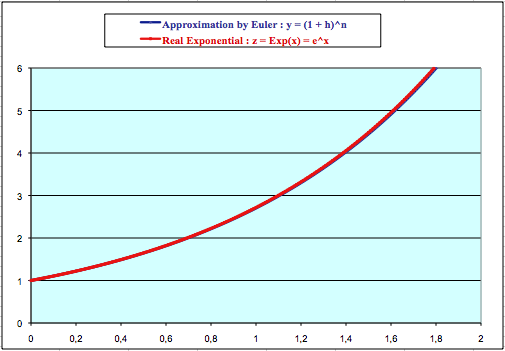
Euler's method
of construction of the Exponential function
[with use of the Computer
Spreadsheet]
- From the differential
equation :
f(a+
h) ≈ f(a) + h.f '(a)
with the initial conditions
f '(x) = f(x)
and f(0) = 1
-
-
Let

-
then
for h = 1/100 and k be an Integer :
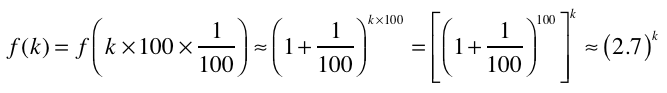
-
then we may
generalize to any real number x :
f(x)
=
ex
f is then called Exponential function : Exp.
-
Fundamental
property of the Exponential
from the hypothesis f '(x)
= f(x) and f(0)
= 1
we prove that for any Real
numbers
u&v Exp(u + v)
=
Exp(u) • Exp(v)
Assignment # 9
to be prepared for Tuesday Dec.7th
Applications
of
Euler's
Method
:
- f '(x) = 1 / (1+x2)
and
f(0)
=
0
- f
'(x) = 2x and f(0) = 0
|

|
Visitors from France
Name
|
Title
/
Activity
|
Mr Rémy
JOST
|
Dean of
the General
Inspection of Mathematics,
Ministry of Education, France
|
Mr Claude
SAUVAGEOT
|
Former
Mathematics
teacher,
Evaluation Expert for the Ministry of Education, France
|
Mr Jean-François
CHESNÉ
|
Former
Mathematics
teacher,
Evaluation Expert for the Ministry of Education, France |
Mrs Claude
RENUCCI
|
Head of
the Publications of the
(National
Center of Pedagogical Documentation (CNDP) of France
|
Ms Lola
MILHEM |
Interpreter
Student at 昆明大学
|
Mr Patrice DESENNE
|
Cameraman
Head of the Audio-visual dept
of CNDP
|
with from 景山学校
Workshop
in
the
VIP
Room
on the organization and teachers training at 景
山学校
with
饭校长
(headmaster)
|
Euler's method
[Download .ppt]
Euler's
method
[Download
.pdf
version]
Euler's Biography
(Wikipedia)
Assignment # 9
(Applications of Euler's method)
===============
Steps of the
Demo of
Exp(u+v)
= Exp(u). Exp(v)
- Hypothesis :
f '(x) = f(x) ; f(0)
= 1
- Let F(x) = f(a+x). f(-x)
and prove that F'(x) = 0
then F(x) = f(a) for any x
- f(a+x). f(-x) = f(a) for any x and a
- for a=0 : f(x).f(-x) =1
then by multiplying the previous equation by f(x),
f(a+x) = f(a). f(x)
- Conclusion :
. f(u+v) = f(u) . f(v) .
.
|
Dec. 07
14:25 - 16:05 |
- Presentation of the answers for Ass. # 9
- Complements on the derivative functions :
- f derivable => f continous
- derivative of f(-x)
- derivative of a composite function :
(f[u(x)])'
=
f
'[u(x)] . u'(x)
- Definition of a Differential in one point
- graphic representation
- Examples
- Theorem of the intermediate
values : how to determine an approximate value of the zeroes of
a function : If f is continuous and monotonous
on [a ; b ] and if f(a).f(b) < 0 then
there is one - and only one - number c between a and b
such that f(c) = 0.
- examples in the above function of which the zeroes of
the
derivative and of itself are the zeroes of a 3° polynomial.
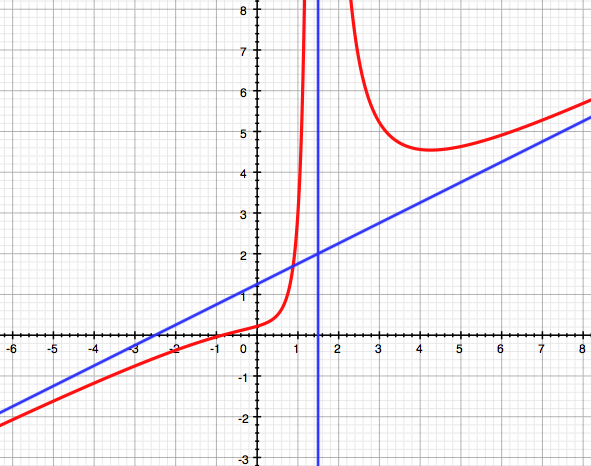
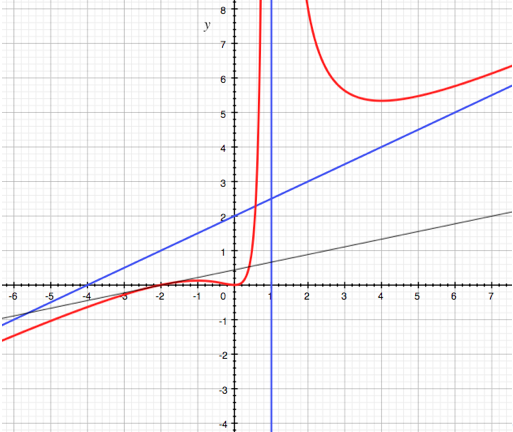
- Review of the general
study of a function :
see models next column.
|
Preparation of Final TEST
- limits
- asymptotes
- derivatives
- tangents
- singular points
- symmetry
- differential
Test
A&B
SOLUTIONS
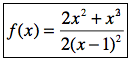
Model of study of a rational
function
[to download]
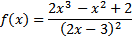
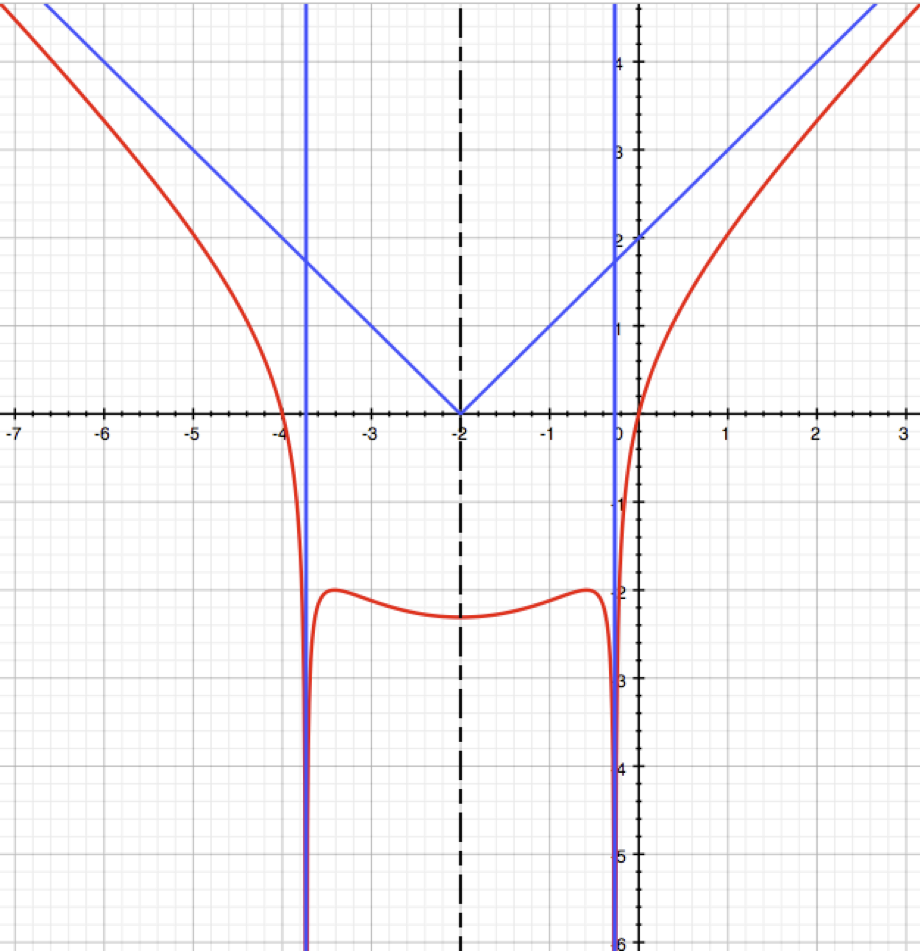
Model study of a non
rationnal function
with axial symmetry
(solution of Ass. # 8 f9)
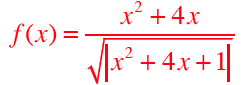
|
|
Test
A&B SOLUTIONS
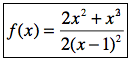
Model of study of a rational
function
[to download]
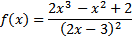
model study of a non
rationnal function
with axial symmetry
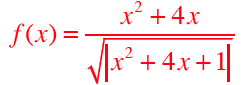
|