jml@ecole-alsacienne.org
<== Sem. Précédente Sommaire Sem. Suivante ==>
Semaine du 20 au 24 février [18]
[dernière mise à jour le : 22/02/06 ]
| Date |
Activités
/ Objectifs |
T.A.F |
Observations |
Références |
|---|---|---|---|---|
Lundi 20 Février 14h-15h |
Cours : Classe entière Exercice de révision sur la "canonisation" du trinôme du second degré et tracé de la Parabole associée. |
Inversion de
l'ordre de passage des groupes de T.D. Gr.1 : Mardi 8h-9h Gr.2 : Mardi 14h-15h |
|
|
|
Mardi 21 Février Gr.I : 8h-9h Gr.II :14h-15h |
TD
: Exercice N°54 p.163 Transformations de la fonction f définie par : y
= f(x) = -(1/2)
x² + 2x + 3
1°) forme y =
a(x - L)² + H2°) forme y = a(x - x')(x - x") 3°) en déduire le sommet, l'intersection avec l'axe Oy, et les intersections avec l'axe Ox, puis construire la Parabole associée. |
Même exercice en partant de la fonction définie par : y = (1/4) (x - x')(x - x") (on pourra déterminer tous les points caractéristiques par calcul mental). |
L'objectif de ces exercices est de pavenir à tracer correctement une parabole associée à n'importe quelle fonction du second degré en moins d'une minute. |
Exercice N°54 p.163 (Hachette 2de / Repères) |
|
Mercredi
22 Février 10h-12h |
Cours : construction de la 3e forme
canonique du trinôme. y =
a(x - x')(x - x")
Exemples d'utilisation des formules Propriétés
algébriques et géométriques de la fonction
définie par :
x----> y
= 1 / x
Construction de la courbe représentative: Hyperbole
Equilatère |
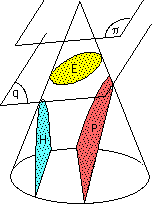 |
Voir les pages web sur
la définition géométrique d'une Parabole et d'une
hyperbole comme intersections d'un cône avec un plan
parallèle à une directrice ou parélléle
à l'axe (Théorèmes d'Apollonius) |
|
| Vendredi 24 Février 9h-10h |
Cours : Définition et
construction des
Hyperboles Equilatères
représentatives
des fonctions du
type
y
= A / x
|